Finnish Rap
The Finnish language is both unique and fascinating, but to an English speaker, it can seem a little jarring with the "H" being pronounced strongly, the trilled "R" and double letters being elongated in words. That said, Finland has some excellent "kotimaiset" (domestic) music. Naturally, the language lends itself quite strongly to heavy metal and this is reflected in the number of metal bands in the country, but radio stations such as Iskelmä play some interesting tunes that are different to the run of the mill noise on UK radio stations.
A poor Outlook
As someone having used GSuite for many years at work, I guess I can call myself a GMail power user. I was dismayed as a decision was taken to move away from GSuite to Office 365 and the Exchange/Outlook combination.
I've found things that were so simple in GMail to be absolute torture in Outlook - searching from all email from a domain now involves the use of complicated search folders instead of typing "from:example.com" in the search bar; delay-sending email is hidden in hierarchies of menus and now spam is handled by a third party rather than just dropping into the "spam" folder for you to decide what to do with it.
Stats...
Benjamin Disreali once said that there were three kinds of lies: Lies, Damned Lies and statistics.
Having been in a number of jobs that need me to use mathematics on a daily basis, when presented with statistics which allegedly prove a point, I'm very quick to ask for the raw data to understand how the statistics were calculated and to check that they're right. I was recently asked to take a look at some road speed statistics and I was given the following data:
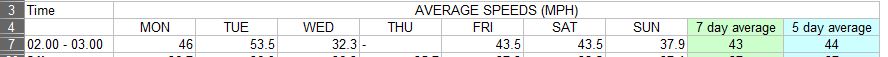
What we have here is a table showing the Mon-Sun average speeds for the 02:00 to 03:00 time block. What the spreadsheet author has done is to sum the average speeds to the left and divide by 7 or 5 to get an average. However this leads to inaccuracies: what we're getting is an average of an average here rather than the true picture. The Monday to Friday sample sizes vary from 0-8 cars and the 8 car hour is getting the same weighting as an hour with just 1 car passing through.
Naturally, I went back to the source of the data and recalcuated using the correct sample size, and this is what I found:

Email Encryption - A Crappy(ta) Solution
Another run in with the local council and the guys at Capita who manage the council tax left me amused. Everytime I contact the council tax guys by email, they insist on responding with some sort of email encryption system.
I'm entirely for email encryption. It's true that the security of email in transit cannot be guaranteed, so any point-to point encryption is an improvement on a pretty flawed system. My preference is for proper encryption such as PGP, but the system employed by Capita positively amuses me - it's all done online on a HTTPS wesbite, but fails to deal with the salient security points. This is my basic analysis:
Build on out...

So; the traffic calming build-out on New Road in Chiseldon is probably going ahead. This is despite my robust objection to the plans, and no real evidence to support it in terms of the road safety or accident reduction being offered. In fact, from a Freedom of Information request I put into the Borough Council, I found that over the last 10 years there have been 12 recorded accidents along the road, of which only one occurred in the vicinity of the proposed build-out. In that single incident, it was unlikely that the cause was attributable to speed and thus any build-out installed probably would not have prevented its occurrence.
Fly Me Away...
Another one of my jaunts to Finland, and unfortunately British Airways didn't offer me the best price. That's no great problem because the national flag carrier, Finnair is pretty good value. Over the years I've used many airlines including some of the low cost carriers such as Ryanair, EazyJet and FlyBe. I have no issues with these outfits as they have their uses, but I dislike the pricing model where luggage, check-in, food on board etc are seen as extras. I was disappointed last time with Finnair to find that they had reduced the food offering down to a sandwich however for an extra £8 or so I could buy the meal 'perk' back. I also saw that they were doing some hand luggage only deals which reminded me of the low cost cowboys.
Blast from the past... Mini Disc

Just dug out a pre-recorded mini-disc which hasn't seen the daylight for years - Savage Garden - Affirmation. Fired up the old mini-disc player which stil works after all these years, although the play button is a little sticky now.
When you look at the mini-disc, they'd pretty much got the whole digital recording thing spot on. It's a shame it was a little too late to market - as MP3s and CDRs began to take off. That said; I'm still using VHS!
Back in Spain
It's about 25 degrees Celsius here on the Costa del Sol as I type this blog. While I haven't kept away from Spain entirely; I've had a jaunt to both Barcelona and Alicante in the last six or so years; I've deliberately kept away from Benalmadena and the Costa del Sol given the fact that I spent a lot of time here as a kid and I believed that "I'd done it all".
Returning to a place that I'd spent 6 to 7 weeks of my life each year between 1987 and 1994 was odd; I calculated that the last time I would have been here was in 2004 when I did a few things for my grandad, and brought a close friend with me. I had no wish to come back after that, but recently I had a hankering to walk down memory lane and look at some of the old places that I used to hang out in as a kid.
While the apartment that my grandparents lived in was in a tourist area, Nan and Grandad were sufficiently resident enough that we were relatively isolated from many of the touristy things. I'm staying in a hotel here this time, and a tourist one at that which is a bit of an eyeopener for me. I tend to go to places off the beaten track, so to be in a hotel with a large number of Brits is for me, at least, quite unusual. I'm honestly unimpressed with my kinfolk - loud, rude and inconsiderate are all adjectives that come to mind, and it is a shame for me to see the Spanish culture being eroded by these idiots that come out here for a cheap package holiday. Few people I saw could even order a beer in Spanish, and often all people wanted to do was lie around a pool and not really move outside of the hotel complex.
On Your Side

It has been years since Nationwide dropped the Anglia part of their name. I remember every Saturday popping into the branch in West Bromwich with my Mum so she could withdraw cash. Ah, those were the days, when you knew the cashier and they knew you.
Benalmadena
My family have had a long relationship with Spain, and in particular Benalmadena. In the late seventies and early eighties, my grandparents on my mother's side had apartments in Arroyo-de-la-Miel and Torremolinos. Both died before I was five years old, and one of the apartments stayed in the family. In 1986, my grandparents on my father's side decided to move out to Spain to live. I remember the day that they flew out and how devastated I was, but the perk was that when the six week school summer holidays, both my sister and I were shipped out on a plane as unaccompanied minors to spend the entire holiday with Gran and Grandad. Sun, a pool and a fairly long leash meant a lot of good memories, good friends and fun.
